Ausgangssituation

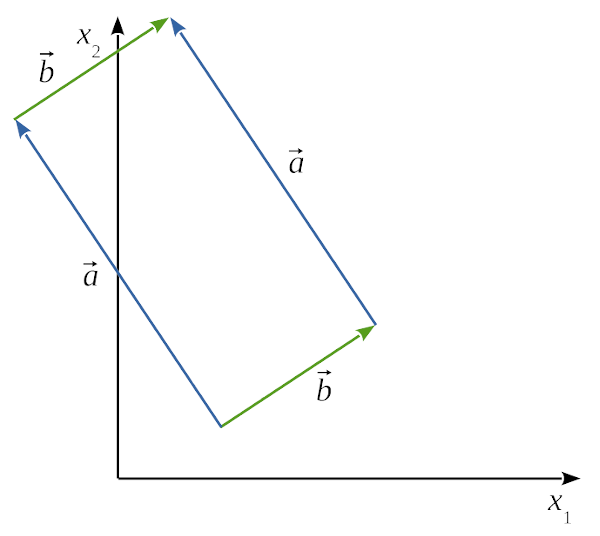
Folgendes Schaubild zeigt die Vektoren $\vec{a} = \begin{pmatrix}-4\\6\end{pmatrix}$ und $\vec{b} = \begin{pmatrix}3\\2\end{pmatrix}$ .

Forschungsauftrag

Beschreibe, welche Form von den Vektoren eingeschlossen wird.

Rechteck

Untersuche die Seiten, Diagonalen und Winkel der Figur.

Die jeweils gegenüber liegenden Seiten sind gleich lang. Beide Diagonalen sind gleich lang. Alle Innenwinklen sind 90° groß.

Bestimme die Vektoren, die den Diagonalen entsprechen.

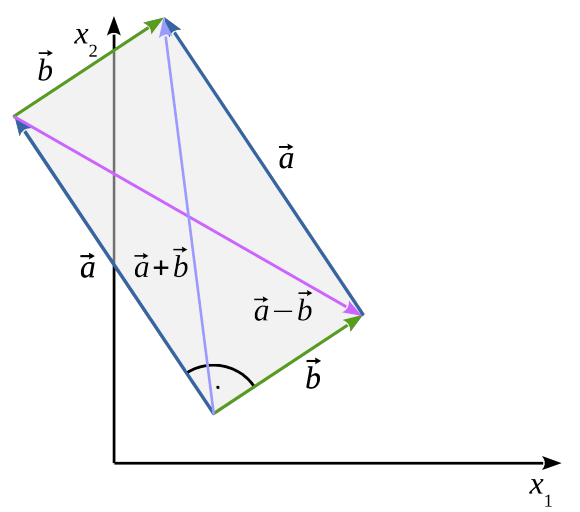
$\vec{d_1} = \vec{a} + \vec{b} = \begin{pmatrix}-4\\6\end{pmatrix} + \begin{pmatrix}3\\2\end{pmatrix} = \begin{pmatrix}-1\\8\end{pmatrix}$

$\vec{d_2} = \vec{a} - \vec{b} = \begin{pmatrix}-4\\6\end{pmatrix} - \begin{pmatrix}3\\2\end{pmatrix} = \begin{pmatrix}-7\\4\end{pmatrix}$

Schlussfolgerungen

Angenommen zwei Vektoren $\vec{a}$ und $\vec{b}$ gehen vom selben Punkt aus.

Gib an wie groß der Winkel ist, den $\vec{a}$ und $\vec{b}$ einschließen, wenn gilt: $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} |$ (d.h. die Diagonalen gleich lang sind).

90°

Bringe die Umforumgen in die richtige Reihenfolge und vollziehe sie nach.

Transfer in den Raum

Gegeben sind die Punkte $P(5|4|10)$ , $Q(12|5|5,5)$ und $S(3|9|8)$ .

Forschungsauftrag

Stelle eine Vermutung auf, ob die Vektoren $\vec{v} = \vec{PQ}$ und $\vec{s} = \vec{PS}$ orthogonal (senkrecht) zueinander sind ( $\vec{v} \perp \vec{s}$ ).
Bestimme die Vektoren $\vec{v}$ und $\vec{s}$ .

$\vec{v} = \begin{pmatrix}7\\1\\-4,5\end{pmatrix}$ $\vec{s} = \begin{pmatrix}-2\\5\\-2\end{pmatrix}$

Übertrag die Schlussfolgerung aus dem zweidimensionalen Raum (siehe oben) auf den dreidimensionalen Raum und zeige rechnerisch am Beispiel von $\vec{v}$ und $\vec{s}$ , dass die Bedingung ebenfalls gilt.

$\vec{v} \cdot \vec{s} = \begin{pmatrix}7\\1\\-4,5\end{pmatrix} \cdot \begin{pmatrix}-2\\5\\-2\end{pmatrix}=7\cdot(-2)+1\cdot5+(-4,5)\cdot(-2)=0$

Definition

Das Produkt zweier Vektoren

$\vec{a} \cdot \vec{b} = \begin{pmatrix}a_1\\a_2\\\vdots\\a_n\end{pmatrix} \cdot \begin{pmatrix}b_1\\b_2\\\vdots\\b_n\end{pmatrix} = a_1 \cdot b_1 + a_2 \cdot b_2 + \dots + a_n \cdot b_n$

heißt Skalarprodukt.

Satz

Zwei Vektoren $\vec{a}$ und $\vec{b}$ sind orthogonal zueinander $(\vec{a} \perp \vec{b})$ , wenn

$\vec{a} \cdot \vec{b} = \dots$

Ergänze die vorstehende Gleichung.

$\vec{a} \cdot \vec{b} = a_1 \cdot b_1 + a_2 \cdot b_2 + \dots + a_n \cdot b_n = 0$