Von der Änderung zum Bestand: Übungen

Übung 1: Autofahrt

Ein Auto fährt mit einer konstanten Geschwindigkeit von $v(t)=100 \, \frac{km}{h}$ auf einer geraden Straße.

Skizziere den Graphen der Geschwindigkeit in Abhängigkeit von der Zeit in einem Koordinatensystem.

Zeichne ein Koorinatensystem. Auf der x-Achse trägst du die Zeit in Stunden und auf der y-Achse die Geschwindigkeit in $\frac{km}{h}$ dar.

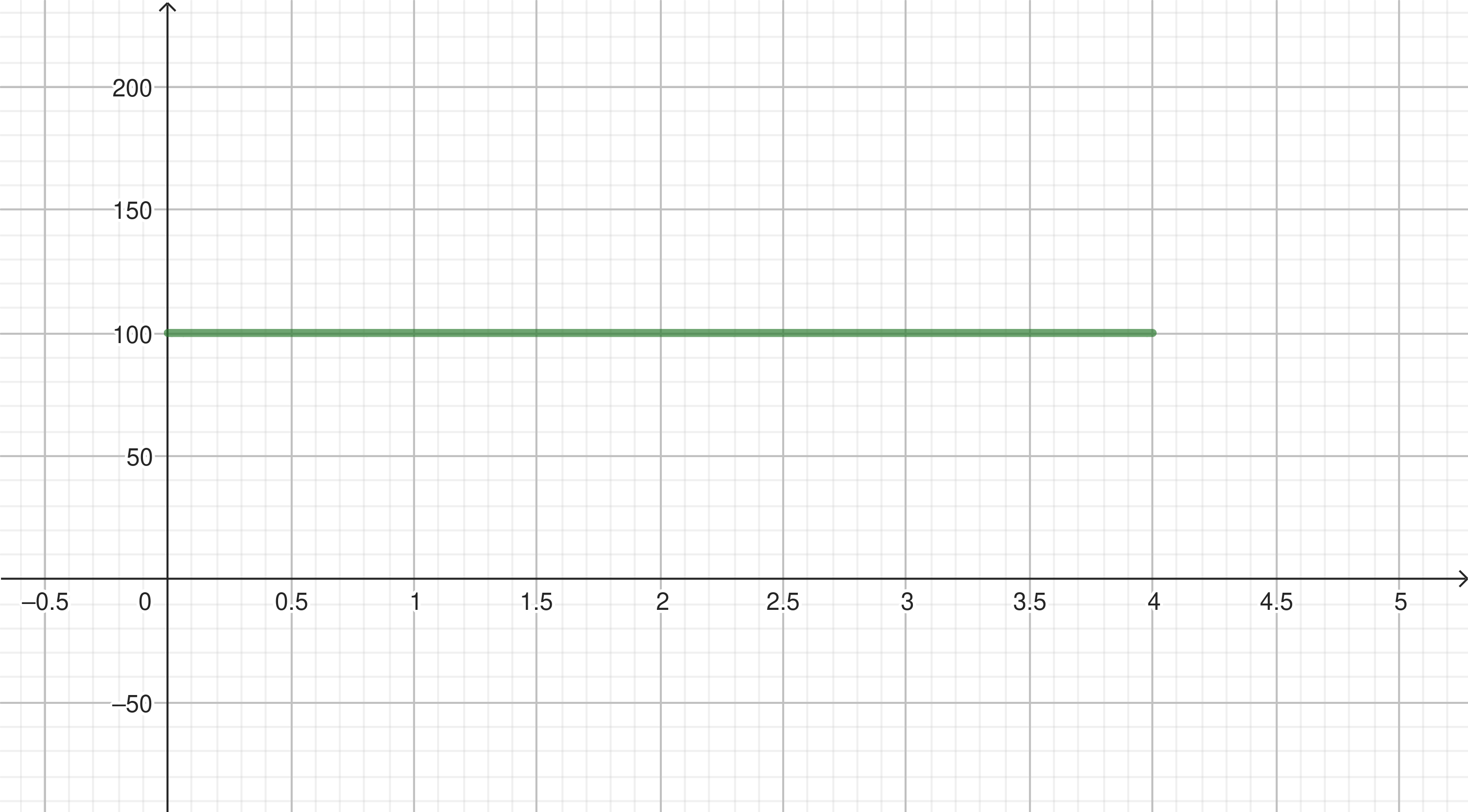
Berechne die Strecke, die das Auto in den ersten 2 Stunden zurücklegt.

$s = 100 \cdot 2 = 200$

Antwort: Das Auto legt in den ersten 2 Stunden 200 km zurück.

Stelle die zurückgelegte Strecke im Koordinatensystem dar.

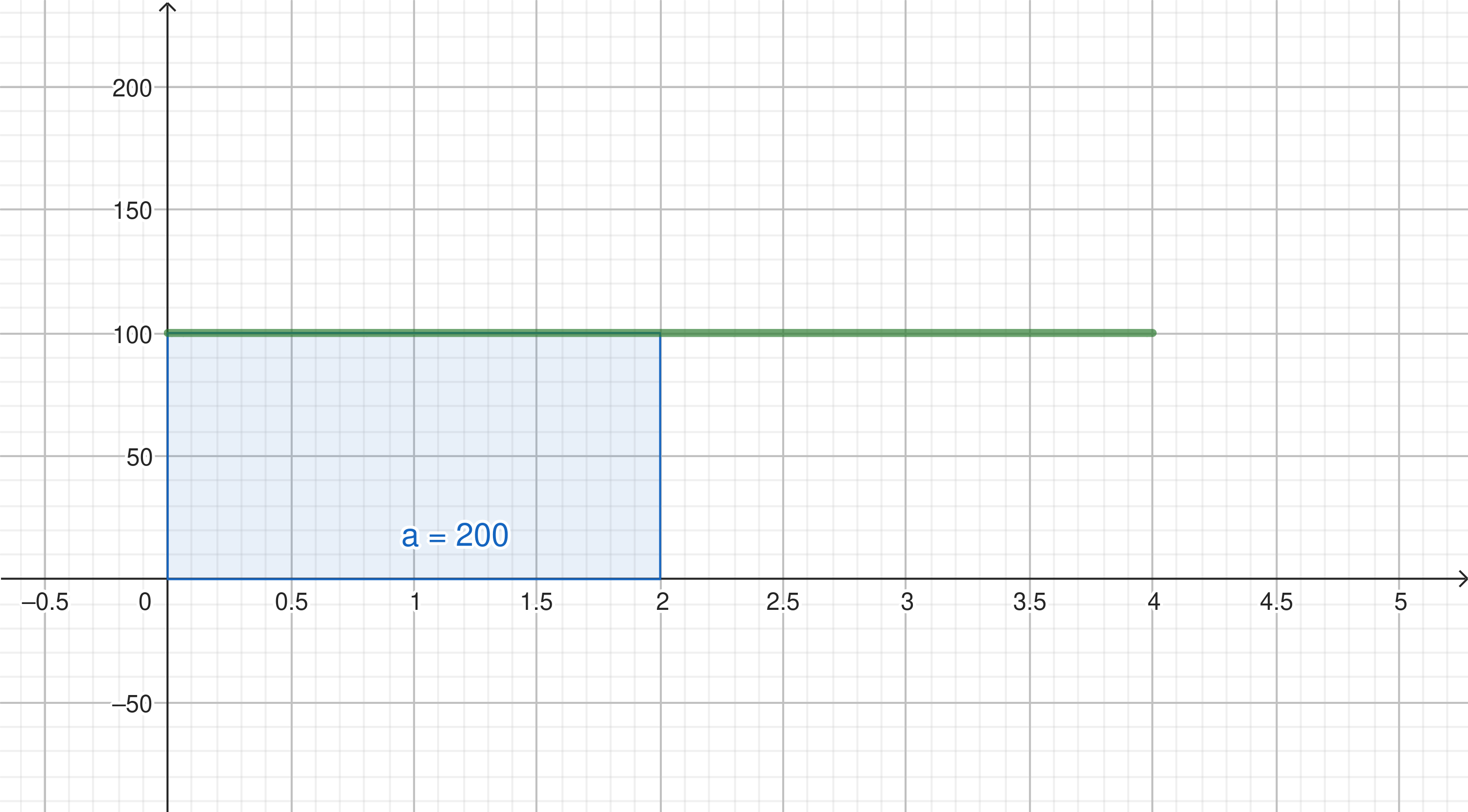
Übung 2: Schwimmbad

Ein Schwimmbad füllt sich in den ersten 30 Minuten mit 20 Besuchern pro Stunde. Danach steigt der Zufluss an Besuchern in den nächsten 30 Minuten linear auf 40 Besucher pro Stunde an.

Skizziere den Graphen der Anzahl der Besucher in Abhängigkeit von der Zeit in einem Koordinatensystem.

Zeichne ein Koorinatensystem. Auf der x-Achse trägst du die Zeit in Stunden und auf der y-Achse den Zufluss an Besuchern in $\frac{Besucher}{Minuten}$ dar.

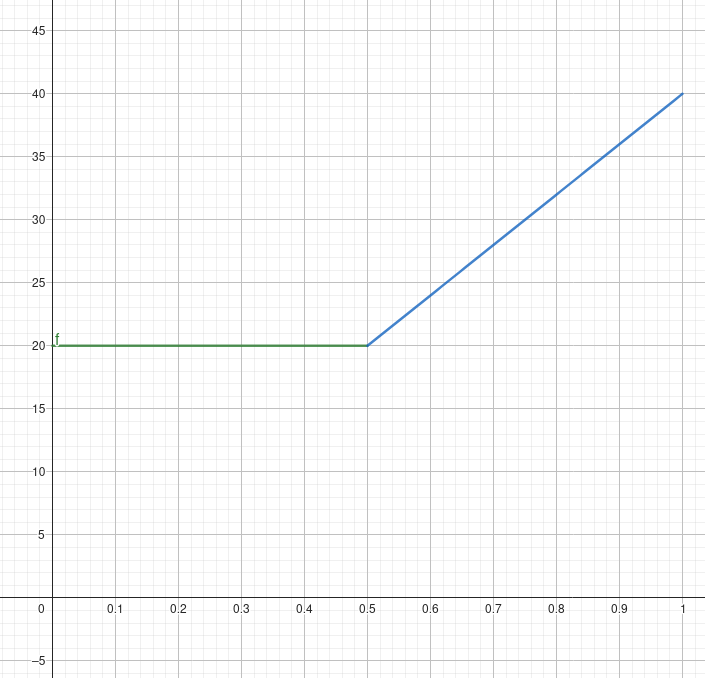
Berechne die Anzahl der Besucher nach 1 Stunde.

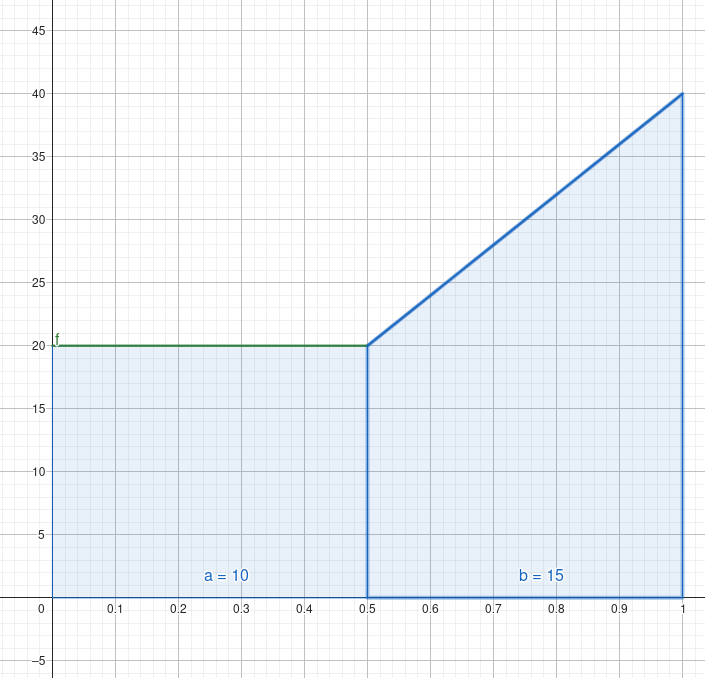
Stelle die Fläche zwischen dem Graphen und der x-Achse als Flächen dar. Benutze Rechtecke und Dreiecke.

Die Fläche a ist ein Rechteck mit den Seitenlängen 20 und 0,5 und die Fläche b ist eine zusammengesetzte Fläche aus einem Rechteck mit den Seitenlängen 20 und 0,5 und einem Dreieck mit der Grundseite 0,5 und der Höhe 20.

\begin{align*} a &= 20 \cdot 0,5 = 10 \\ b &= 20 \cdot 0,5 + \frac{1}{2} \cdot 0,5 \cdot 20 = 15 \\ c &= a + b = 25 \end{align*}

Übung 3: Fritzchens Bergwanderung

Fritzchen macht an einem sonnigen Ferientag eine Bergwanderung. Von einem Freund hat er eine Tour empfohlen und zur mentalen Vorbereitung ein Diagramm erstellt bekommen. Darin hat der Freund (geringfügig vereinfacht) die Zuordnung Zeit (in h) → Steiggeschwindigkeit (in m/h) für diese Wanderung dargestellt.

Fritzchen beginnt seine Wanderung um 10 Uhr vormittags.

Variieren Sie in dem Applet den Wert für k und betrachten Sie, wie sich Punkt P verändert. Beachten Sie auch die Beschriftung der Achsen!

Begründe, dass der abgebildete Graph nicht das Höhenprofil der Wanderung darstellt.

Ein Höhenprofil zeigt die Höhe in Abhängigkeit von der zurückgelegten Strecke.

Die Werte auf der y-Achse beschreiben nicht die bei der Wanderung erreichte Höhe, sondern die sog. "Steiggeschwindigkeit", mit der Fritzchen zu diesem Zeitpunkt läuft.

Interpretiere im Sachkontext, dass der Graph für $1<x<3$ konstant verläuft. Gib auch den Höhenunterschied an, den Fritzchen in dieser Zeit zurücklegt.

Im Intervall $1<x<3$ , also in einem Zeitraum von zwei Stunden, beträgt die Anstiegsgeschwindigkeit konstant 300m/h. Also überwindet Fritzchen in diesem Zeitraum insgesamt 600 Höhenmeter.

Fritzchen plant, eine Pause einzulegen, wenn er den höchsten Punkt der Wanderung erreicht hat. Bestimme die Uhrzeit, an der Fritzchen diese voraussichtlich einlegen wird. Begründe deine Antwort.

Bis zum Zeitpunkt x=4 (also bis 14 Uhr) ist Fritzchens Steiggeschwindigkeit größer als Null, er geht also bis dahin immer bergauf. Erst zum Zeitpunkt x=4 ist die Steiggeschwindigkeit erstmals Null. Der Anstieg ist dann beendet. In der folgenden Stunde wird Fritzchen weiterhin keinen Anstieg haben, es könnte also auch sein, dass er im Zeitraum zwischen 14 und 15 Uhr weitere Rastplätze mit guter Aussicht findet.

Betrachte den Graphen und prüfe die folgenden Aussagen:
1. Fritzchen beginnt seine Wanderung bei 0 Metern über dem Meeresspiegel.
2. Fritzchen steigt in der ersten Stunde seiner Wanderung relativ steil an, kann sich dann aber in den folgenden zwei Stunden entspannen, weil der Weg dann nur waagerecht verläuft.
3. In den ersten vier Stunden seiner Wanderung steigt Fritzchen (ggf. unterschiedlich steil) den Berg hoch.
4. Nach fünf Stunden steigt Fritzchen in ein Tal ab und klettert in der letzten Stunde seiner Wanderung (also im Interall $7<x<8$ ) auf der anderen Seite des Tals den Hang wieder hinauf.
5. Fritzchen steigt in der ersten Stunde 300 m hoch.
6. Fritzchen steigt in der ersten Stunde 600 m hoch.
7. Fritzchen steigt in der ersten Stunde 150 m hoch.

iii und vii sind korrekt.

Berechne, wie viel Höhenmeter Fritzchen in den ersten 4 Stunden seiner Wanderung zurücklegt.

Er ist in den ersten 4 Stunden 900 m hoch gestiegen.

Übung 4: Hubschrauber

Ein Hubschrauber startet zur Zeit $t = 0 s$ vom Boden. Die Geschwindigkeit des Hubschraubers in vertikaler Richtung wird durch das folgende Diagramm beschrieben. Dabei wird die Zeit t in Sekunden (s) und die Geschwindig- keit v in Meter pro Sekunde (m/s) angegeben.

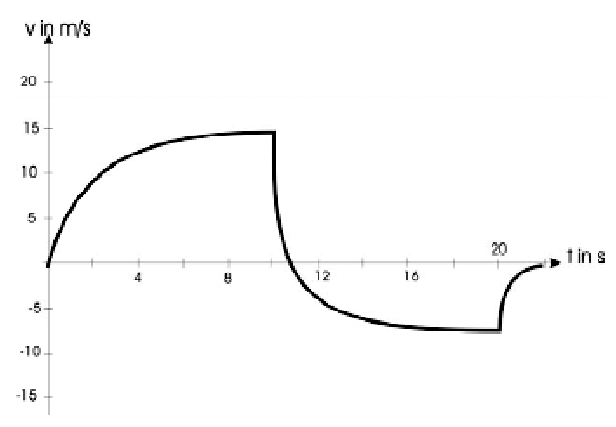
Beschreibe den Bewegungsablauf ohne Rechnung.
1. In welchen Zeitabschnitten bewegt sich der Hubschrauber aufwärts bzw. abwärts?
2. Zu welchen Zeitpunkten ändert der Hubschrauber die Bewegungsrichtung?
3. Wann war die Steiggeschwindigkeit am größten?
4. Wann war die Sinkgeschwindigkeit am größten?

Graph von f oberhalb der t-Achse: Hubschrauber bewegt sich nach oben für $0 \leq t \leq 11$
Graph von f unterhalb der t-Achse: Hubschrauber bewegt sich nach unten für $11 \leq t \leq 22$
Schnittpunkte des Graphen von f mit der t-Achse: dort Änderung der Bewegungsrichtung: t = 11
Hochpunkt des Graphen von f: größte Steiggeschwindigkeit (t = 10)
Tiefpunkt des Graphen von f: größte Sinkgeschwindigkeit (t = 20)

In welchen Zeitabschnitten des Steigflugs findet eine positive bzw. negative Beschleunigung statt?

positive Steigung des Graphen von f: positive Beschleunigung für $0 \leq t \leq 10$
negative Steigung des Graphen von f: negative Beschleunigung für $10 \leq t \leq 11$ Lösungsansätze sind z. B. qualitatives differenzieren des Graphen bzw. erkennen der Beschleunigung als Änderungsrate der Geschwindigkeit.

Bestimme eine sinnvolle Schätzung für die nach 10 Sekunden erreichte Höhe.

Die näherungsweise Berechnung, z. B. über Rechteck- oder Trapezsummen, ergibt eine Höhe von ca. 108 m. Ebenfalls möglich wäre eine Argumentation mit der mittleren Geschwindigkeit (etwa 10 m/s). Damit ergibt sich eine Höhe von ca. 100 m.

Interpretation des Integrals als Wirkung (hier: zurückgelegte Höhe)

Nach 22 Sekunden Flugzeit landet der Hubschrauber. Begründe, dass der Landeplatz auf einem Hügel liegt.

Der Flächeninhalt oberhalb der t-Achse ist größer als unterhalb der t-Achse, d. h. die zurückgelegte Strecke nach oben ist größer als die zurückgelegte Strecke nach unten.

Interpretation des Integrals als Bilanzierung von Flächeninhalten