Unter- und Obersumme per Hand berechnen

Übung 1

Berechne die Unter- und Obersumme von $f(x)=\frac{1}{5}x^2$ für 10 Rechtecke gleicher Breite im Intervall $[0, 5]$ händisch in deinem Heft.

• Mache zunächst eine Skizze des Funktionsgraphens und der Rechtecke.
• Beim händischen Berechnen der Summen kannst du die folgende Formel verwenden:

$$1 + 2^2 + 3^2 + \ldots + n^2 = \frac{n(n+1)(2n+1)}{6}$$

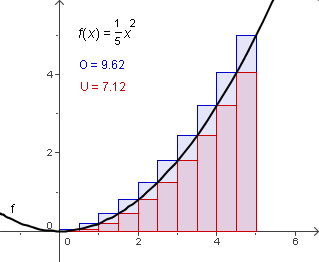
• Gib auch das arithmetische Mittel von Unter- und Obersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an.

Übung 2

Berechne für $f(x)=1,2^x$ die Unter- und Obersumme für 10 Rechtecke gleicher Breite im Intervall $[0, 10]$ in deinem Heft.

• Mache auch hier eine Skizze des Funktionsgraphens und der Rechtecke.
• Du kannst bei der Berechnung der Summen die folgende Formel verwenden:

$$1 + q^1 + q^2 + \ldots + q^n = \frac{q^{n}-1}{q-1}$$

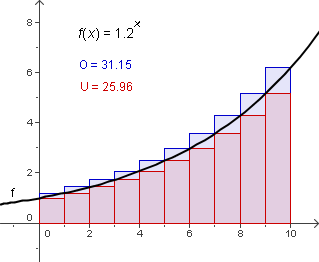
• Gib auch das arithmetische Mittel von Unter- und Obersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an.

Unter- und Obersumme per Hand berechnen