Das Flächenproblem

Das Flächenproblem ist ein zentrales Problem in der Mathematik und ein wichtiger Anwendungsfall der Integralrechnung. Es geht darum, die Fläche unter einem Funktionsgraphen zu berechnen.

Beispiel: Der Flächeninhalt eines Grundstücks

Das Bauamt einer Großstadt hat beschlossen, die im Stadtplan grün eingezeichnete Fläche südlich des Flusses neu zu gestalten. Doch für die Planungsarbeiten muss zuerst einmal die Größe des Grundstücks ermittelt werden. Wie groß ist der Flächeninhalt dieses Grundstückes ungefähr?

Aufgaben

Die drei Punkte $P_1$, $P_2$ und $P_3$ legen eine Polynomfunktion 2. Grades fest.

1. Versuche den Flächeninhalt mithilfe des Rasters näherungsweise abzu­schätzen.
2. Setze die drei Punkte $P_1$, $P_2$ und $P_3$ so auf das Flussufer, dass der Graph der (quadratischen) Funktion damit zur Deckung kommt. Lies ab wie groß der Flächeninhalt ungefähr ist.
3. Bonus: Kann es im Allgemeinen überhaupt gelingen, den Graphen einer Polynomfunktion 2. Grades mit einem beliebig verlaufenden Flussufer zur Deckung zu bringen?

Beispiel: Wasserverbrauch während einer Fußballübertragung

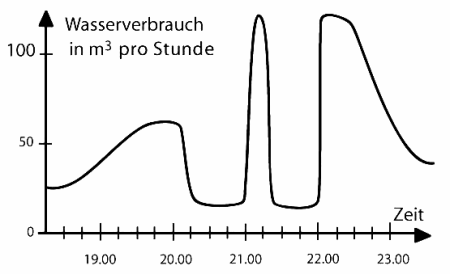
Am Abend der Fernsehübertragung eines Fußballspiels der Champions League wurde der Wasserverbrauch in einer Stadt gemessen. Die folgende Grafik zeigt den Verlauf des Wasserverbrauchs in Litern pro Stunde:

Aufgaben

1. Bestimme das Ende der ersten Halbzeit.
2. Bestimme, wann das Spiel zu Ende gewesen ist.
3. Schätze wie groß der Gesamtverbrauch während der Pause gewesen ist.
4. Schätze wie groß der Gesamtverbrauch während der gesamten Fernsehübertragung gewesen ist.
5. Erläutere deinen bei 3. und 4. gewählten Weg zur Berechnung des Gesamtwasserverbrauchs.

Das Flächenproblem