Flächenberechnung mit GeoGebra

In dieser Übung berechnest du Flächen mit Geogebra. Dazu bietet GeoGebra die Funktion Integral(f(x), a, b) an, die das bestimmte Integral der Funktion $f(x)$ im Intervall $[a, b]$ berechnet.

Musterbeispiel

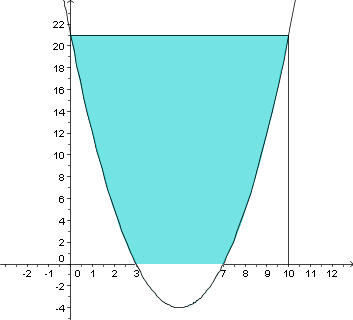
Wir berechnen die in der Abbildung gekennzeichnete Fläche unter dem Graphen der Funktion $f(x) = x^2 -4x +5$ mit GeoGebra.

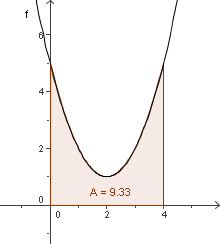
• Wir lesen das Intervall $[0,4]$ aus der Abbildung ab.
• Wir berechnen mit GeoGebra das bestimmte Integral von $f(x)$ in diesem Intervall. Dazu geben wir folgende Befehle ein:
  • f(x) = x^2 -4x +5
  • A = Integral(f,0,4).
• Lösung: Die gekennzeichnete Fläche ist 9.33 [FE] groß.

Aufgaben

Berechne für die folgenden Funktionen die farbig gekennzeichnete Fläche mit GeoGebra.

• Überlege genau, welche bestimmten Integrale dir helfen, die Lösung zu bekommen. Eventuell musst du auch Flächen voneinander subtrahieren oder addieren.
• Schreib alle Ergebnisse zusammen mit einer Skizze in dein Heft.

Aufgabe A

$$f(x) = \sqrt(x)$$

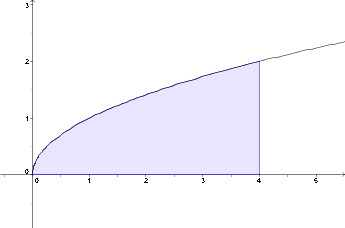
Aufgabe B

$$f(x) = 0,5x^2$$

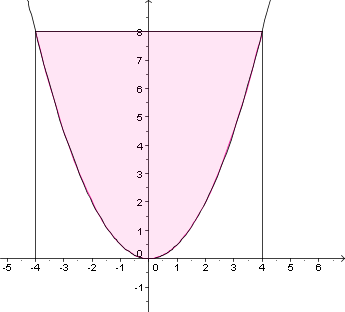
Aufgabe C

$$f(x) = 3-x^2$$

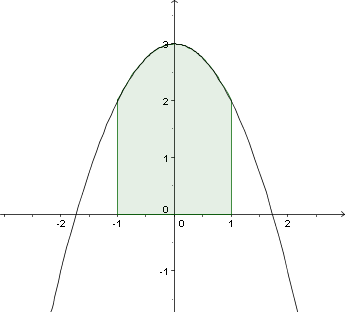
Aufgabe D

$$f(x) = (x-5)^2-4$$

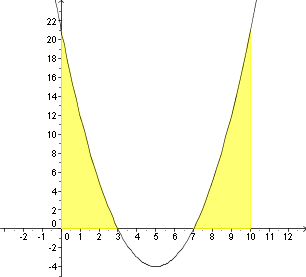
Aufgabe E

$$f(x) = (x-5)^2 -4$$

💻 Flächenberechnung mit GeoGebra